Transformer 模型已在包括自然语言、对话、图像甚至音乐在内的各种领域取得了最先进的成果。每个 Transformer 架构的核心模块都是注意力模块,它计算输入序列中所有位置对的相似度得分。然而,这很难与输入序列的长度相匹配,需要二次计算时间来生成所有相似度得分,以及二次内存大小来构建一个矩阵来存储这些得分。
对于需要远程注意力的应用,已经提出了几种快速且更节省空间的代理,例如内存缓存技术,但更常见的方法是依赖稀疏注意力。稀疏注意力通过从序列而不是所有可能的对中计算有限的相似度得分来减少计算时间和注意力机制的内存要求,从而得到稀疏矩阵而不是完整矩阵。这些稀疏条目可以手动提出,通过优化方法找到,学习,甚至随机化,如稀疏变换器,长形变换器,路由变换器, 改革者和大鸟等方法所证明的那样。由于稀疏矩阵也可以用图和边表示,稀疏化方法也受到图神经网络文献的启发,与图注意力网络中概述的注意力的具体关系。这种基于稀疏性的架构通常需要额外的层来隐式产生完整的注意力机制。
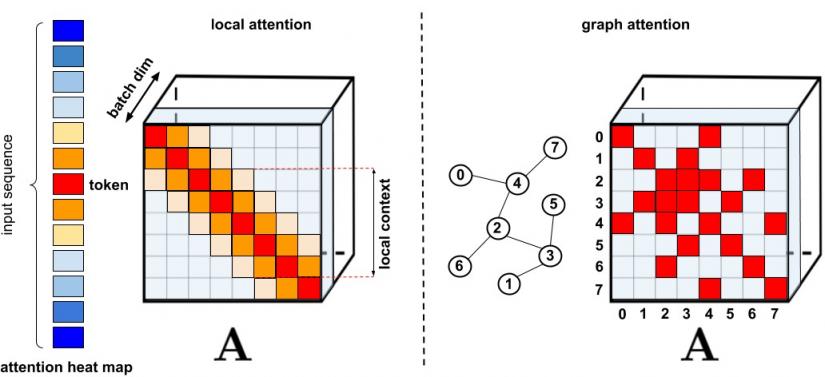
标准稀疏化技术。左图:稀疏模式示例,其中 token 仅关注其他附近的 token。右图:在图注意力网络中,token 仅关注图中的邻居,这些邻居的相关性应高于其他节点。请参阅《高效 Transformers:综述》以全面了解各种方法。
不幸的是,稀疏注意力方法仍然存在许多限制。(1)它们需要高效的稀疏矩阵乘法运算,而并非所有加速器都具备这种运算;(2)它们通常不为其表示能力提供严格的理论保证;(3)它们主要针对 Transformer 模型和生成式预训练进行优化;(4)它们通常会堆叠更多的注意力层来弥补稀疏表示,这使得它们难以与其他预训练模型一起使用,因此需要重新训练并消耗大量能源。除了这些缺点之外,稀疏注意力机制通常仍然不足以解决常规注意力方法所应用的所有问题,例如指针网络。还有一些操作无法稀疏化,例如常用的softmax 操作,它在注意力机制中对相似度得分进行归一化,在工业规模的推荐系统中被大量使用。
为了解决这些问题,我们引入了Performer,这是一种 Transformer 架构,其注意力机制可线性扩展,从而实现更快的训练,同时允许模型处理更长的长度,这是某些图像数据集(如ImageNet64)和文本数据集(如PG-19)的要求。 Performer 使用高效(线性)广义注意力框架,该框架允许基于不同相似性度量(核)的广泛注意力机制。 该框架由我们新颖的通过正正交随机特征实现的快速注意力 (FAVOR+) 算法实现,该算法提供可扩展的低方差和无偏注意力机制估计,可通过随机特征图分解(特别是常规 softmax 注意力)来表达。 我们为该方法获得了强大的准确度保证,同时保持了线性空间和时间复杂度,这也可以应用于独立的 softmax 操作。
广义注意力机制
在原始的注意力机制中,查询和密钥输入分别对应矩阵的行和列,它们相乘并通过 softmax 运算形成注意力矩阵,用于存储相似度得分。请注意,在此方法中,将查询-密钥乘积传递到非线性 softmax 运算后,无法将其分解回原始查询和密钥组件。但是,可以将注意力矩阵分解回原始查询和密钥的随机非线性函数 的乘积(也称为随机特征),从而允许以更有效的方式对相似度信息进行编码。
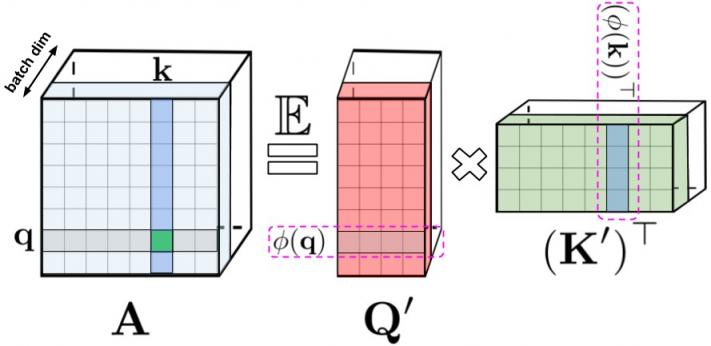
LHS:标准注意矩阵,包含每对条目的所有相似度得分,由查询和键上的 softmax 运算形成,表示为q和k。RHS :标准注意矩阵可以通过低秩随机矩阵Q′和K′来近似,其中行编码原始查询/键的潜在随机非线性函数。对于常规的 softmax 注意力,变换非常紧凑,涉及指数函数以及随机高斯投影。
常规 softmax-attention 可以看作是这些非线性函数的一种特殊情况,这些非线性函数由指数函数和高斯投影定义。请注意,我们也可以反向推理,首先实现更一般的非线性函数,在查询键乘积上隐式定义其他类型的相似性度量或核。我们将其定义为广义注意力,基于核方法的早期工作。虽然对于大多数内核来说,闭式公式并不存在,但我们的机制仍然可以应用,因为它不依赖于它们。
据我们所知,我们是第一个证明任何注意力矩阵都可以在下游 Transformer 应用中使用随机特征进行有效近似的人。实现这一点的新机制是使用正随机特征,即原始查询和键的正值非线性函数,这对于避免训练期间的不稳定至关重要,并且可以更准确地近似常规 softmax 注意力机制。
迈向 FAVOR+:通过矩阵关联性实现快速注意力
上述分解允许以线性而非二次方的内存复杂度存储隐式注意力矩阵。使用这种分解还可以获得线性时间注意力机制。虽然原始注意力机制将存储的注意力矩阵与值输入相乘以获得最终结果,但在分解注意力矩阵后,可以重新排列矩阵乘法以近似常规注意力机制的结果,而无需明确构建二次方大小的注意力矩阵。这最终导致了FAVOR+。
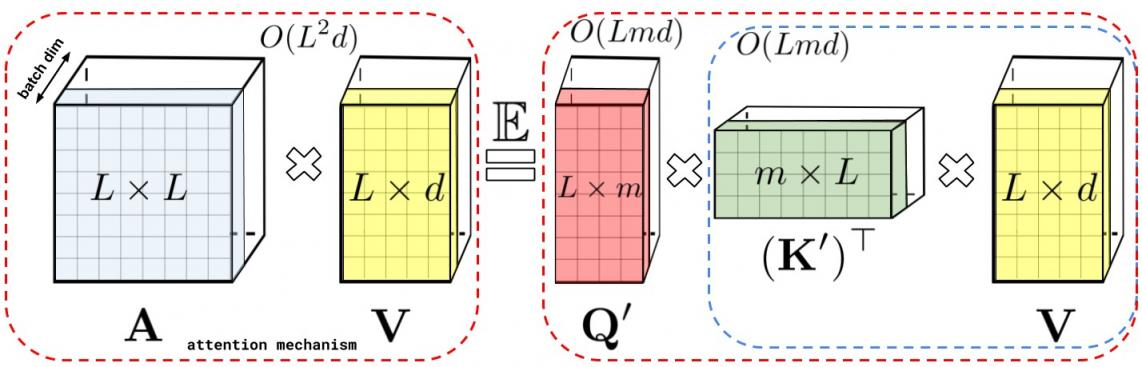
左图:标准注意力模块计算,最终期望结果通过对注意力矩阵A和值张量V进行矩阵乘法计算得出。右图:通过解耦A低秩分解中使用的矩阵Q′和K′,并按照虚线框所示的顺序进行矩阵乘法,我们得到了一种线性注意力机制,从不明确构造A或其近似值。
上述分析与所谓的双向注意力相关,即没有过去和未来概念的非因果注意力。对于单向(因果)注意力,即标记不会关注输入序列中稍后出现的其他标记,我们稍微修改了使用前缀和计算的方法,它只存储矩阵计算的运行总数,而不是存储明确的下三角常规注意力矩阵。
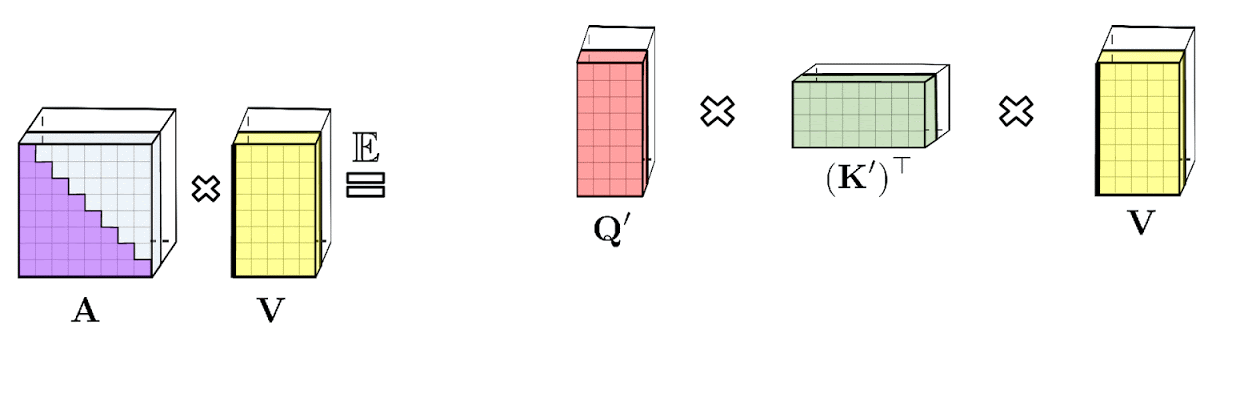
左图:标准单向注意力需要屏蔽注意力矩阵以获得其下三角部分。右图:可以通过前缀和机制获得 LHS 上的无偏近似,其中动态构建键和值向量的随机特征图外积的前缀和,并将其左乘以查询随机特征向量以获得结果矩阵中的新行。
属性
我们首先对表演者的空间和时间复杂度进行基准测试,并表明注意力加速和内存减少在经验上几乎是最佳的,即非常接近在模型中根本不使用注意力机制。
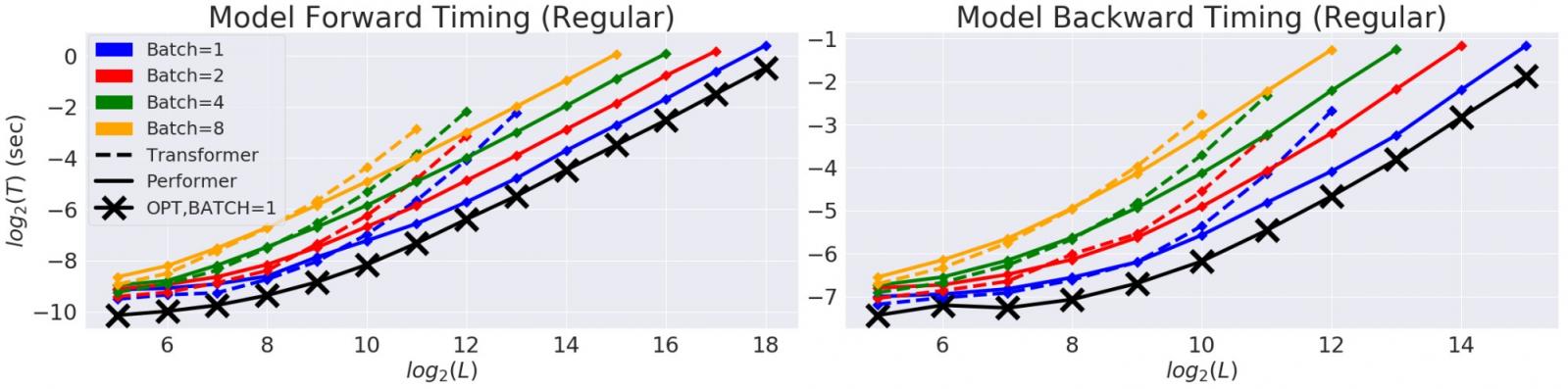
常规 Transformer 模型的双向计时以对数对数图表示,时间 ( T ) 和长度 ( L )。线条在 GPU 内存的极限处结束。黑线 (X) 表示使用“虚拟”注意力模块时可能实现的最大内存压缩和加速,这实质上绕过了注意力计算并展示了模型的最大效率。Performer 模型几乎能够在注意力组件中达到这种最佳性能。
我们进一步表明,使用我们的无偏 softmax 近似,Performer 经过一些微调后可以向后兼容预训练的 Transformer 模型,这可以通过提高推理速度来降低能源成本,而无需完全重新训练预先存在的模型。
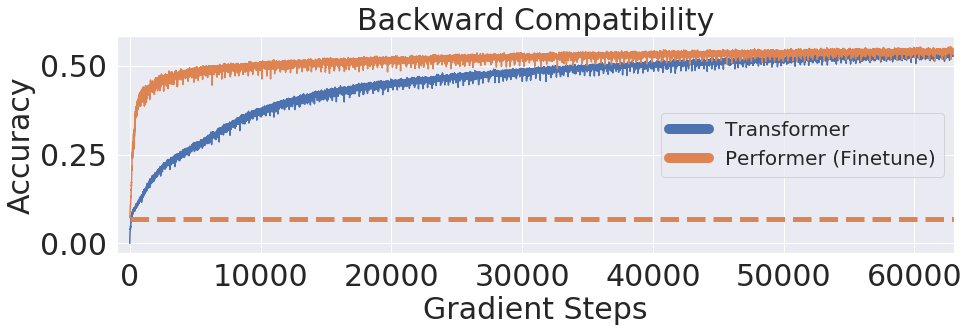
使用十亿词基准(LM1B) 数据集,我们将原始预训练的 Transformer 权重转移到 Performer 模型,该模型产生了初始非零的 0.07 准确率(橙色虚线)。然而,一旦进行微调,Performer 便会以原始梯度步骤数的一小部分快速恢复准确率。
示例应用:蛋白质建模
蛋白质是具有复杂 3D 结构和特定功能的大分子,对生命至关重要。与单词一样,蛋白质被指定为线性序列,其中每个字符是 20 种氨基酸构建块之一。将 Transformers 应用于大量未标记的蛋白质序列语料库(例如UniRef)可产生可用于对折叠的功能性大分子进行准确预测的模型。Performer-ReLU(使用基于ReLU的注意力,这是与 softmax 不同的广义注意力的一个实例)在建模蛋白质序列数据方面表现强劲,而 Performer-Softmax 与 Transformer 的性能相匹配,正如我们的理论结果所预测的那样。
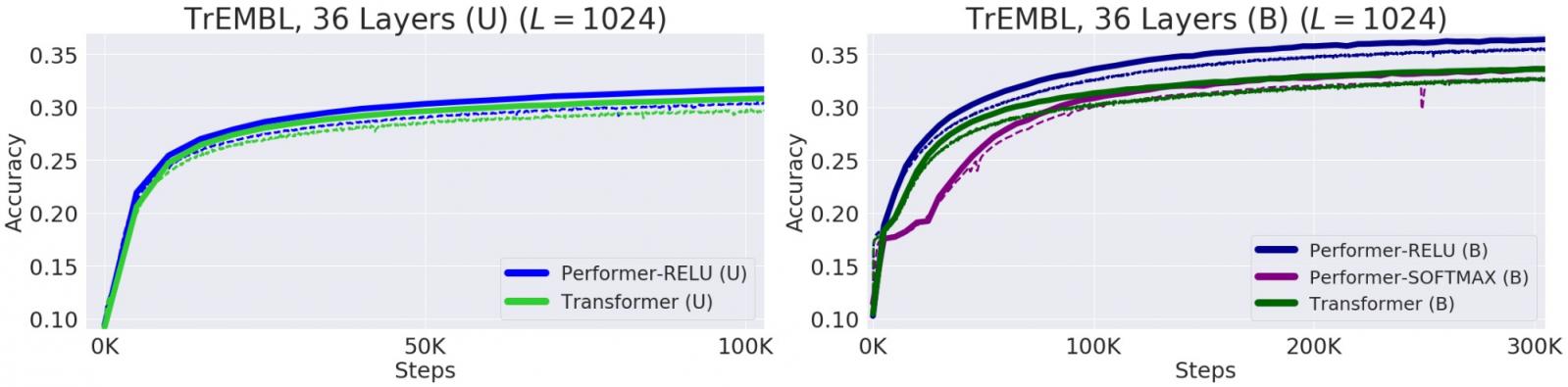
蛋白质序列建模性能。训练 = 虚线,验证 = 实线,单向 = (U),双向 = (B)。我们在所有运行中均使用ProGen (2019)中的 36 层模型参数,每次运行均使用 16x16 TPU-v2。考虑到相应的计算约束,每次运行的批次大小均最大化。
下面我们可视化了一个使用基于 ReLU 的近似注意力机制训练的蛋白质 Performer 模型。使用 Performer 估计氨基酸之间的相似性可以恢复与通过分析精心策划的序列比对中的进化替换模式获得的众所周知的替换矩阵相似的结构。更一般地说,我们发现局部和全局注意力模式与在蛋白质数据上训练的 Transformer 模型一致。Performer 的密集注意力近似有可能捕捉多个蛋白质序列之间的全局相互作用。作为概念证明,我们在长连接蛋白质序列上训练模型,这会使常规 Transformer 模型的内存过载,但由于其空间效率,Performer 不会过载。
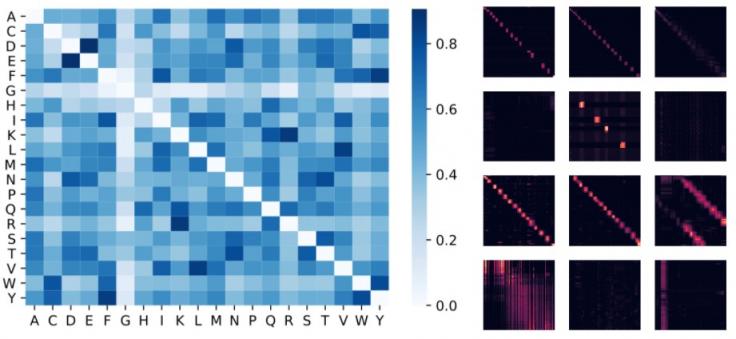
左图:根据注意力权重估计的氨基酸相似性矩阵。尽管该模型只能访问蛋白质序列而没有关于生物化学的先验信息,但它可以识别高度相似的氨基酸对,例如 (D,E) 和 (F,Y)。中间图:BPT1_BOVIN蛋白质的 4 个层(行)和 3 个选定头部(列)的注意力矩阵,显示了局部和全局注意力模式。
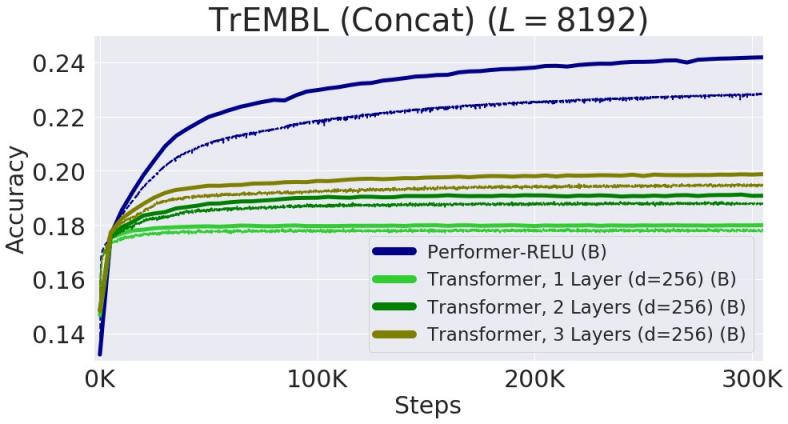
通过连接单个蛋白质序列获得的长度高达 8192 的序列的性能。为了适应 TPU 内存,Transformer 的大小(层数和嵌入维度)有所减小。
结论我们的工作为最近在非稀疏性方法和基于内核的 Transformers 解释方面的
努力做出了贡献。我们的方法可以与可逆层等其他技术互操作,我们甚至将FAVOR 与 Reformer 的代码集成在一起。我们提供论文、Performer 代码和蛋白质语言建模代码的链接。我们相信我们的研究开辟了一种全新的思维方式,可以思考注意力、Transformer 架构甚至内核方法。
致谢
这项工作由核心 Performer 设计师 Krzysztof Choromanski(Google Brain 团队,技术和研究主管)、Valerii Likhosherstov(剑桥大学)和 Xingyou Song(Google Brain 团队)完成,David Dohan、Andreea Gane、Tamas Sarlos、Peter Hawkins、Jared Davis、Afroz Mohiuddin、Lukasz Kaiser、David Belanger、Lucy Colwell 和 Adrian Weller 也做出了贡献。我们特别感谢应用科学团队共同领导将高效 Transformer 架构应用于蛋白质序列数据的研究工作。
我们还要感谢 Joshua Meier、John Platt 和 Tom Weingarten 就生物数据进行的多次富有成效的讨论以及对本草案的有益评论,以及 Yi Tay 和 Mostafa Dehghani 就比较基线进行的讨论。我们还要感谢 Nikita Kitaev 和 Wojciech Gajewski 就 Reformer 进行的多次讨论,以及 Aurko Roy 和 Ashish Vaswani 就 Routing Transformer 进行的多次讨论。
评论