世界上最快的超级计算机是为模拟物理现象而设计的,但它们的速度仍然不足以稳健地预测气候变化的影响、设计基于气流的飞机控制装置或准确模拟聚变反应堆。所有这些现象都由偏微分方程(PDE) 建模,偏微分方程是描述物理世界中所有平滑和连续事物的方程类,也是科学和工程中最常见的一类模拟问题。为了解决这些方程,我们需要更快的模拟,但近年来,摩尔定律一直在放缓。与此同时,我们看到机器学习 (ML) 取得了巨大突破,以及为其优化的更快硬件。这种新范式为科学计算提供了什么?在发表于《美国国家科学院院刊》的
“学习数据驱动的偏微分方程离散化”中,我们探索了 ML 如何持续改进高性能计算的潜在途径,既可以用于解决 PDE,也更广泛地用于解决每个科学领域的难题。 对于大多数实际问题,偏微分方程并不存在闭式解。相反,必须找到计算机可以求解的离散方程(“离散化” ),以近似连续偏微分方程。求解偏微分方程的典型方法表示网格上的方程,例如使用有限差分。为了实现收敛,网格的网格间距需要小于解的最小特征尺寸。这通常是不可行的,因为不良的缩放定律:实现 10 倍更高的分辨率需要 10,000 倍更多的计算,因为网格必须在四个维度上缩放——三个空间维度和时间。相反,我们在论文中表明,ML 可用于在更粗的网格上学习偏微分方程的更好表示。

飓风的卫星照片,采用 最先进天气模型的全分辨率和模拟分辨率。积云(例如,红色圆圈内)是造成强降雨的原因,但在天气模型中,细节完全模糊了。相反,模型依赖于亚网格物理的粗略近似,这是气候模型中不确定性的主要来源。图片来源:NOAA
挑战在于在使用尽可能粗的网格的同时保持高分辨率模拟的准确性。在我们的工作中,我们能够改进现有方案,用基于机器学习的优化规则取代基于人类深刻洞察力的启发式方法(例如,“PDE 的解决方案应该始终平滑地远离不连续性”)。我们的 ML 模型恢复的规则很复杂,我们并不完全了解它们,但它们结合了复杂的物理原理,例如“逆风”的概念——为了准确模拟流体流动中迎面而来的风,您应该顺着风吹来的方向向上游看。下面显示了我们在一个简单的流体动力学模型上得到的结果示例:
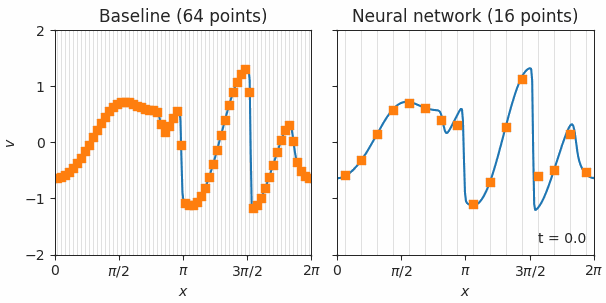
伯格斯方程的模拟,流体中的冲击波模型,用标准有限体积法(左)或基于神经网络的方法(右)求解。橙色方块表示在低分辨率网格上使用每种方法进行的模拟。这些点在每个时间步骤中被反馈到模型中,然后模型预测它们应该如何变化。蓝线显示用于训练的精确模拟。神经网络解决方案要好得多,即使在 4 倍粗的网格上也是如此,如橙色方块平滑地追踪蓝线所示。
我们的研究还阐明了如何有效地将机器学习与物理学结合起来的更广泛的教训。我们不是试图从头开始学习物理学,而是将神经网络与传统模拟方法的组成部分结合起来,包括我们正在求解的方程的已知形式和有限体积法。这意味着,通过构造,动量守恒定律等定律得到了完全满足,并允许我们的机器学习模型专注于它们最擅长的领域,学习在复杂的高维空间中进行插值的最佳规则。
下一步
我们专注于扩大论文中概述的技术,以解决对现实世界有影响的更大规模的模拟问题,例如天气和气候预测。我们对将机器学习融入科学计算的复杂算法的广泛潜力感到兴奋。
致谢
感谢共同作者 Yohai Bar-Sinari、Jason Hickey 和 Michael Brenner;以及 Google 合作者 Peyman Milanfar、Pascal Getreur、Ignacio Garcia Dorado、Dmitrii Kochkov、Jiawei Zhuang 和 Anton Geraschenko。
评论