机器学习 (ML) 算法生成的模型的质量直接取决于训练数据的质量,但现实世界的数据集通常包含一定量的噪声,这会给 ML 模型带来挑战。数据集中的噪声有多种形式,从损坏的样本(例如,猫图像中的镜头光晕)到数据收集时标记错误的样本(例如,猫图像被错误地标记为flerken)。ML
模型处理嘈杂训练数据的能力在很大程度上取决于训练过程中使用的损失函数。对于分类任务,用于训练的标准损失函数是逻辑损失。然而,由于两个不良特性,这种特定的损失函数在处理嘈杂的训练示例时会失效:
远处的异常值可能会主导整体损失:逻辑损失函数对异常值很敏感。这是因为当错误标记的示例(异常值)远离决策边界时,损失函数值会无限增长。因此,远离决策边界的单个坏示例可能会对训练过程造成惩罚,以至于最终训练的模型会学会通过拉伸决策边界并可能牺牲剩余的好示例来弥补这一点。下图左侧面板说明了这种“大幅度”噪声问题。
附近错误标记的示例可能会拉长决策边界:神经网络的输出是激活值向量,它反映了每个类别的示例与决策边界之间的边距。softmax传递函数用于将激活值转换为示例属于每个类别的概率。由于此逻辑损失传递函数的尾部以指数级快速衰减,训练过程将倾向于将边界拉近到更接近错误标记的示例,以补偿其较小的边距。因此,即使标签噪声水平较低(下图右图),网络的泛化性能也会立即恶化。
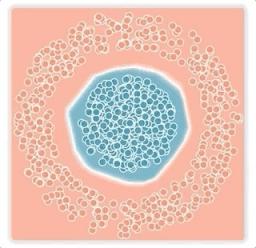

我们将训练二元分类的 2 层神经网络的决策面可视化。蓝点和橙点代表两个类别的示例。该网络在两种噪声条件下使用逻辑损失进行训练:(左)大边距噪声和(右)小边距噪声。
在最近的一篇论文中,我们引入了一种“双调”广义逻辑损失函数,该函数具有两个可调参数,可以很好地处理这些情况,我们称之为“温度”—— t 1表示有界性,t 2表示尾部沉重性(即传递函数尾部的下降率)。这些属性如下所示。将t 1和t 2都设置为 1.0 可以恢复逻辑损失函数。将t 1设置为低于 1.0 会增加有界性,而将t 2设置为大于 1.0 会使传递函数尾部更重。我们还推出了这种交互式可视化功能,让您可以直观地看到具有双调逻辑损失的神经网络训练过程。
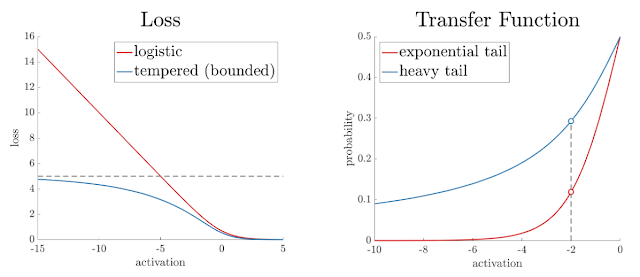
左图:损失函数的有界性。当 t 1介于 0 和 1 之间(不包括 0 和 1)时,即使每个示例被错误标记,也只会产生有限量的损失。图中显示 t 1 = 0.8。右图:传递函数的尾部重度。当 t 2 = > 1.0时,重尾传递函数适用,并为相同数量的激活分配更高的概率,从而防止边界更接近噪声示例。图中显示 t 2 = 2.0。
为了展示每种温度的影响,我们在一个合成数据集上训练了一个两层前馈神经网络,用于二分类问题,该数据集包含来自第一类的一圈点和来自第二类的一圈同心圆点。您可以在浏览器上使用我们的交互式可视化亲自尝试。我们使用标准逻辑损失函数(可以通过将两个温度都设置为 1.0 来恢复)以及我们的双温度逻辑损失来训练网络。然后,我们针对干净数据集、具有小幅度噪声的数据集、大幅度噪声和具有随机噪声的数据集展示每种损失函数的影响。
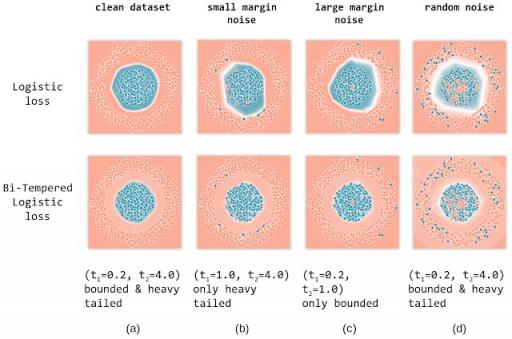
逻辑损失与双调节逻辑损失:(a)无噪声标签,(b)小边距标签噪声,(c)大边距标签噪声,以及(d)随机标签噪声。每个图上方显示了调节损失的温度值(t 1,t 2)。我们发现,对于每种情况,使用双调节逻辑损失函数进行训练恢复的决策边界都比以前更好。
无噪声情况:
我们在 (a) 列中展示了在无噪声数据集上使用逻辑损失(顶部)和双调节逻辑损失(底部)训练模型的结果。白线显示每个模型的决策边界。双调节损失函数中的温度( t 1,t 2 )的值显示在图的每一列下方。请注意,对于这种温度选择,损失是有界的,传递函数是尾部较重的。可以看出,这两种损失都产生了良好的决策边界,成功地将两个类分开。
小边际噪声:
为了说明概率尾部较重的影响,我们人为地破坏了决策边界附近的随机示例子集,也就是说,我们将这些点的标签翻转为相反的类。 (b) 列显示了使用逻辑损失和双调节损失在具有小边际噪声的数据上训练网络的结果。
可以看出,由于 softmax 尾部较轻,逻辑损失将边界拉近噪声点以补偿其低概率。另一方面,仅使用尾部较重概率传递函数的双调节损失通过调整t 2可以成功避开噪声示例。这可以通过调节指数函数的较重尾部来解释,该函数分配了相当高的概率值(从而保持损失值较小),同时保持决策边界远离噪声示例。
大边际噪声:
接下来,我们评估两个损失函数处理大边际噪声示例的性能。在 (c) 中,我们随机破坏远离决策边界的示例子集(环的外侧以及靠近中心的点)。
对于这种情况,我们仅使用双调节损失的有界性,同时保持 softmax 概率与逻辑损失相同。逻辑损失的无界性导致决策边界向噪声点扩展,以降低其损失值。另一方面,有界的双调节损失(通过调整t 1来限制)对每个噪声示例产生有限的损失。因此,双调节损失可以避开这些噪声示例并保持良好的决策边界。
随机噪声:
最后,我们研究训练数据中的随机噪声对两个损失函数的影响。请注意,随机噪声包括小边距和大边距噪声示例。因此,我们通过将温度设置为 ( t)来利用双调节损失函数的有界性和尾部重量特性。1 , t 2 ) = (0.2, 4.0)。
从最后一列 (d) 的结果可以看出,逻辑损失受噪声示例的影响很大,显然无法收敛到良好的决策边界。另一方面,双调节可以恢复与无噪声情况几乎相同的决策边界。
结论
在这项工作中,我们构建了一个有界的调节损失函数,可以处理大边际异常值,并在我们的新调节 softmax 函数中引入了重尾性,该函数可以处理小边际错误标记的示例。使用我们的双调节逻辑损失,我们在许多大型标准数据集上训练神经网络时取得了出色的经验性能(有关详细信息,请参阅我们的论文)。请注意,最先进的神经网络已经与各种变量一起进行了优化,例如:架构、传递函数、优化器选择和标签平滑等等。我们的方法引入了两个额外的可调变量,即( t 1, t 2)。我们相信,通过对所有常用变量进行系统性的“联合优化”,可以与我们的损失函数一起实现显著的进一步改进。这当然是一个更长远的目标。我们还计划探索在训练过程中退火温度参数的想法。
致谢:
这篇博文反映了我们与合著者Manfred Warmuth(客座研究员)和Tomer Koren(谷歌研究高级研究员)的合作。我们的论文预印本可在此处获得,其中包含损失函数的理论分析和大规模标准数据集的实证结果。
评论