许多传统机器学习 (ML) 侧重于利用可用数据做出更准确的预测。最近,研究人员考虑了其他重要目标,例如如何设计小型、高效和稳健的算法。考虑到这些目标,一个自然的研究目标是在神经网络之上设计一个系统,该系统可以有效地存储编码在其中的信息——换句话说,是一种计算复杂深度网络如何处理其输入的简洁摘要(“草图”)的机制。草图是一个丰富的研究领域,可以追溯到Alon、Matias 和 Szegedy 的基础工作,它可以使神经网络有效地总结有关其输入的信息。
例如:想象一下走进一个房间并简要查看其中的物体。现代机器学习非常擅长回答在训练时已知的关于这个场景的即时问题:“有猫吗?这只猫有多大?”现在,假设我们在一年中每天都看这个房间。人们可以回忆起他们看到这个房间的次数:“房间里有猫的频率是多少?”我们通常是在早上还是晚上看到房间?”。但是,是否可以设计出能够有效回答此类基于记忆的问题的系统,即使在训练时这些问题是未知的?
上发表的 “模块化深度学习的递归草图”中,我们探讨了如何简洁地总结机器学习模型如何理解其输入。我们通过使用计算的“草图”来扩充现有(已经训练过的)机器学习模型来实现这一点,使用它们来有效地回答基于记忆的问题(例如,图像到图像的相似性和汇总统计数据),尽管它们占用的内存比存储整个原始计算要少得多。基本草图算法 通常,草图算法采用向量x并生成输出草图向量,该向量的行为与 x 相似,但存储成本要小得多。存储成本小得多这一事实使得人们可以简洁地存储有关网络的信息,这对于有效回答基于记忆的问题至关重要。在最简单的情况下,线性草图x由矩阵向量乘积Ax给出,其中A是一个宽矩阵,即列数等于x的原始维度,行数等于新的缩减维度。此类方法已导致各种高效算法
用于海量数据集上的基本任务,例如估计基本统计数据(例如,直方图、分位数和四分位距)、查找热门项目(称为频繁元素),以及估计不同元素的数量(称为支持大小)和相关的规范和熵估计任务。
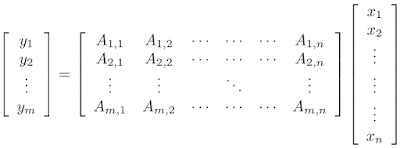
绘制向量 x 的一个简单方法 是将其乘以宽矩阵 A 以生成低维向量 y。
这种基本方法在相对简单的线性回归 情况下效果很好,在这种情况下,只需通过权重的大小就可以识别重要的数据维度(通常假设它们具有均匀方差)。然而,许多现代机器学习模型实际上是深度神经网络,基于高维嵌入(如Word2Vec、Image Embeddings、Glove、DeepWalk和BERT),这使得总结模型对输入的操作变得更加困难。然而,这些更复杂的网络中很大一部分是模块化的,尽管它们很复杂,但我们能够生成其行为的准确草图。
神经网络模块化模块化深度网络
由几个独立的神经网络(模块)组成,它们仅通过将一个网络的输出作为另一个网络的输入进行通信。这个概念启发了几种实用的架构,包括神经模块化网络、胶囊神经网络和PathNet。也可以拆分其他规范架构以将它们视为模块化网络并应用我们的方法。例如,传统上,卷积神经网络(CNN) 被理解为以模块化方式运行;它们在较低层检测基本概念和属性,并在较高层检测更复杂的对象。从这个角度来看,卷积核对应于模块。下面给出了模块化网络的卡通描述。
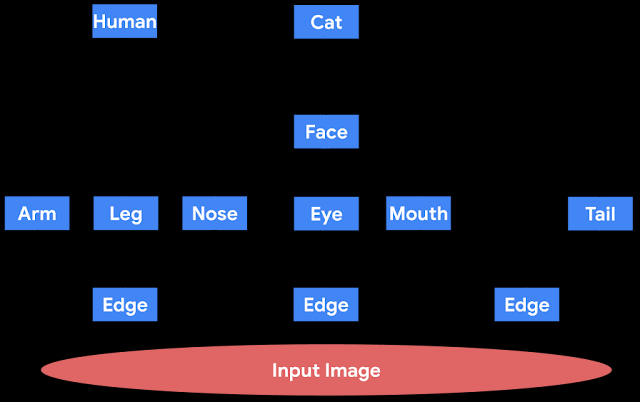
这是用于图像处理的模块化网络的卡通图。数据通过用蓝色方框表示的模块从图的底部流向顶部。请注意,较低层的模块对应于基本对象,例如图像中的边缘,而较高层的模块对应于更复杂的对象,例如人类或猫。还请注意,在这个虚构的模块化网络中,人脸模块的输出足够通用,可供人类和猫模块使用。
草图要求
为了优化这些模块化网络的方法,我们确定了网络草图应该满足的几个期望属性:
草图到草图的相似性: 两个不相关的网络操作的草图(无论是就当前模块而言还是就属性向量而言)应该非常不同;另一方面,两个相似的网络操作的草图应该非常接近。
属性恢复: 属性向量,例如,图中任何节点的激活都可以从顶层草图中近似恢复。
摘要统计: 如果有多个相似对象,我们可以恢复有关它们的摘要统计信息。例如,如果一张图片有多只猫,我们可以计算出有多少只。请注意,我们想在事先不知道问题的情况下做到这一点。
优雅擦除:擦除顶层草图的后缀可保留上述属性(但会平滑地增加错误)。
网络恢复:给定足够多的(输入,草图)对,可以近似地恢复网络边缘的布线以及草图功能。
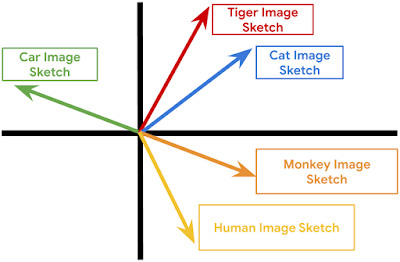
这是草图与草图相似性的 2D 卡通描述。每个向量代表一幅草图,相关草图更有可能聚集在一起。
草图绘制机制
我们提出的草图绘制机制可应用于预训练的模块化网络。它会生成一个单一的顶层草图,总结该网络的运行,同时满足上述所有所需属性。要理解它是如何做到这一点的,首先考虑一个单层网络会有所帮助。在这种情况下,我们确保与特定节点有关的所有信息都“打包”到两个单独的子空间中,一个对应于节点本身,一个对应于其相关模块。使用合适的投影,第一个子空间让我们可以恢复节点的属性,而第二个子空间则有助于快速估计汇总统计数据。这两个子空间都有助于强化上述草图到草图的相似性。我们证明,如果所有涉及的子空间都是随机独立选择的,那么这些属性就成立。
当然,将这个想法扩展到具有多层的网络时必须格外小心——这导致了我们的递归草图绘制机制。由于它们的递归性质,这些草图可以“展开”以识别子组件,甚至捕获复杂的网络结构。最后,我们利用针对我们的设置量身定制的字典学习算法来证明,从足够多的(输入,草图)对中可以恢复构成草图机制和网络架构的随机子空间。
未来方向
简洁地总结网络操作的问题似乎与模型可解释性问题密切相关。研究草图文献中的想法是否可以应用于这个领域将会很有趣。我们的草图也可以组织在存储库中,以隐式形成“知识图谱”,从而可以识别和快速检索模式。此外,我们的草图机制允许无缝地将新模块添加到草图存储库中——探索此功能是否可以应用于架构搜索和不断发展的网络拓扑将会很有趣。 最后,我们的草图可以看作是一种在内存中组织以前遇到的信息的方式,例如,共享相同模块或属性的图像将共享其草图的子组件。从非常高的层次上讲,这类似于人类使用先验知识识别物体并推广到未遇到的情况的方式。
致谢
本工作由 Badih Ghazi、Rina Panigrahy 和 Joshua R. Wang 共同完成。
评论